端子拉力计算公式是什么,端子正向力计算公式介绍
端子正向力通常指的是连接端子或螺栓上的拉力或张力,也就是连接处的拉伸力。从端子的导通性能角度来说,端子的正向力越大,接触电阻越小,导通性能越好,所以,设计员希望较大的正向力。二从端子的装配性能的角度来说,端子的正向力越大,插拔力越大,装配性能越差,因此,设计员希望较小的正向力。
综合二者来看,设计人员设计端子正向力时既不能过大又不能过小,否则会影响端子的正常使用性能。
端子正向力计算公式
计算端子正向力的公式取决于多个因素,包括施加的力、材料的性质以及连接的几何形状。下面是计算端子正向力的一般公式:
端子正向力(T)= 施加的力(F)/ 螺栓或连接材料的截面积(A)
其中:
- T是端子正向力,以牛顿(N)或磅力(lb)为单位。
- F是施加在连接处的拉伸力,以牛顿(N)或磅力(lb)为单位。
- A是螺栓或连接材料的截面积,以平方米(m²)或平方英寸(in²)为单位。
需要注意以下几点:
-
施加的力(F)应考虑方向,只有在拉伸方向上的力才能计算端子的正向力。
-
连接材料的截面积(A)是连接部位的横截面积,通常是圆形螺栓的截面积或连接材料的横截面积,根据实际连接形状来计算。
-
如果连接材料的材质不均匀,需要考虑材料截面积上的变化,通常使用平均截面积进行估算。
-
请注意单位的一致性,确保施加的力、截面积和端子正向力的单位一致。
-
螺栓或连接材料的杨氏模量(弹性模量)也可以影响正向力的计算,特别是在考虑了材料的弹性变形时。这可能需要进行更为复杂的有限元分析。
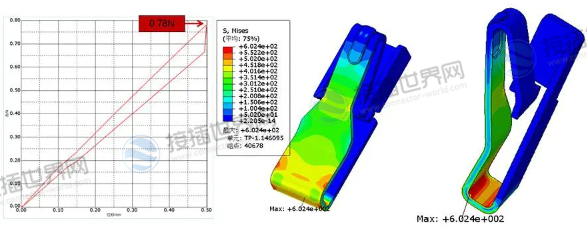
端子正向力悬臂梁模型计算
通常情况下,端子正向力分析常用的悬臂梁模型进行计算,悬臂梁模型常用于估算端子或螺栓的正向拉伸力,这是一种简化的工程分析方法。在这个模型中,悬臂梁代表了螺栓或连接材料的形状,通过应用拉力来估算其正向拉伸力。下面是常用的悬臂梁模型计算公式:
端子正向拉伸力(F)= (d×E×W×t³) / (4×L³)
其中:
- F是端子的正向拉伸力,以牛顿(N)为单位。
- d是螺栓或连接材料的直径,以米(m)为单位。
- E是杨氏模量(弹性模量),描述了材料的弹性性质,以帕斯卡(Pa)为单位。
- W是螺栓或连接材料的截面宽度,以米(m)为单位。
- t是螺栓或连接材料的截面厚度,以米(m)为单位。
- L是悬臂梁的长度,以米(m)为单位。
这个公式基于悬臂梁的弯曲理论,假设连接材料在拉伸时会弯曲,从而产生正向拉伸力。需要注意的是,这个公式是一种简化的模型,通常用于估算。实际应用中,还需要考虑其他因素,如材料的弹性性质、材料的应力-应变曲线、材料的应变硬化行为等。因此,在工程实践中,更复杂的有限元分析可能会用于更准确的正向拉伸力估算。、
此外,要确保使用正确的单位,并根据具体情况对参数进行合适的转换,以确保计算的准确性。如果涉及到重要的结构或设备连接,建议专业人士分析和验证。